疊加原理及其應用

疊加原理

在物理學與系統理論領域，疊加原理闡述了線性系統中，由多個刺激疊加產生的總反應等同於各個單獨刺激所產生反應的代數和，即：

若輸入 A 引發反應 X，輸入 B 產生 Y，則 A+B 的反應等於 (X+Y)。

從數學角度，對於線性系統 F(x)=y，其中的 x 表示刺激（輸入），而 y 表示反應（輸出），刺激的疊加（即「和」）所得出的反應也等同於各個反應的疊加。

疊加原理的應用

疊加原理廣泛應用於許多物理學與工程學領域，因為許多物理系統可以用線性系統建模。比方説，樑結構可視為線性系統，其中輸入刺激是樑上的結構載荷，而輸出反應則為樑的撓度。

需要注意的是，物理系統通常僅為近似線性，疊加原理往往僅是真實物理現象的近似；由此可推測這些系統運作的區域範圍。

疊加原理適用於任何線性系統，包含代數方程式、線性微分方程式以及這些形式的方程組。輸入與反應可以是數字、函數、向量、向量場、時變信號或任何遵循特定公理的其他對象。特別注意，涉及到向量與向量場時，疊加操作為向量和運算。

傅立葉分析

藉由疊加原理，我們可以將線性系統中一個極為一般的刺激分解為一系列特定簡單形式的刺激之疊加，進而簡化反應的計算。舉例來説，在傅立葉分析中，刺激可以表示為無數個正弦波的疊加。由於疊加原理，每個正弦波可以單獨分析，它們各自的反應也可以分別計算出來。（反應本身也是一個正弦波，與刺激頻率相同，但振幅與相位可能不同。）根據疊加原理，原始刺激的反應可以透過所有單一正弦波反應的總和（或積分）來表示。

格林函數分析

另一個常見的範例是格林函數分析，其中刺激可以分解為無數個脈衝函數的疊加，而反應則是脈衝響應的疊加。

疊加原理在波動分析中也十分實用。比如在電磁理論中，光通常被描述為平面波（固定頻率、偏振與方向的波）疊加而成的。若疊加原理成立（通常成立，但並非絕對；請參閲非線性光學），任何光波的行為都可以視為這些基本平面波行為的疊加。

波動中的疊加原理

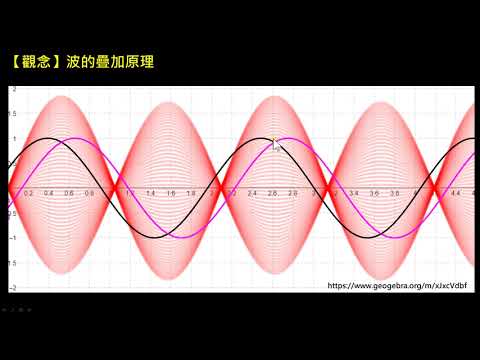
在任何有波動存在的系統中，特定時間的波型取決於系統的激勵源（即可能產出或影響波動的外力）與初始條件。在許多情況下（比如經典波動方程式），用於描述波動的方程式是線性的。當條件滿足時，便可運用疊加原理。這意味著在同一空間傳播的兩個或多個波動，其合成振幅等於每個波動單獨產生振幅之和。例如，兩個相向傳播的波動將會直接穿過彼此，在另一側不會產生任何形變（參閲最上方圖片）。

疊加：意義、特性和應用

疊加是一個物理學名詞，用於描述兩個或更多個波或場以特定方式結合，形成新波或場的現象。疊加的結果取決於波或場的振幅、頻率和相位。

疊加具有以下特性：

• 線性性：疊加的結果與組成波或場的振幅成正比。
• 可逆性：疊加的過程可以被逆轉，組成波或場可以從疊加的結果中分離出來。
• 相干性：對於相干波或場，疊加的結果會因波或場的相位差而改變。

波疊加

波疊加是指兩個或更多個波結合形成新波的現象。新波的性質取決於組成波的振幅、頻率和相位。

• 相長干涉：當具有相同頻率和相位的波疊加時，形成的波具有更高的振幅。
• 相消干涉：當具有相同頻率但相位相反的波疊加時，形成的波具有較低的振幅或甚至消失。
• 部分相長干涉：當具有相同頻率但相位不完全相同的波疊加時，形成的波具有介於相長干涉和相消干涉之間的振幅。

場疊加

場疊加是指兩個或更多個場結合形成新場的現象。新場的性質取決於組成場的振幅、頻率和相位。

• 電磁場疊加：兩個或更多個電磁場疊加後，形成的新電磁場具有這些場的電場和磁場的總和。
• 力場疊加：兩個或更多個力場疊加後，形成的新力場具有這些場的力的總和。
• 量子場疊加：處於疊加態的量子場可以同時處於多個量子狀態，直到被觀測。

疊加的應用

疊加在物理學和工程學的許多領域都有應用，包括：