方位角:指南
方位角(azimuth),又稱方位向、地平經度,是從觀察者的指北方向線,順時針至目標方向線的水平夾角。它在球座標系中,用於測量角度。簡而言之,它是觀測者與目標點向量投影到基準面的正交點,與指北向量形成的角度。
天體中的方位角

天體觀測中,方位角表示天體在地平線上出現的方向。恆星為觀測點,基準面為觀測者所在地區的地球表面,參考向量為正北。方位角則是恆星向量投影於基準面上,與真北向量夾角。
方位角的起源
「方位角」一詞源自阿拉伯語「as-sumūt」,意為「方向」。

陸地導航中的方位角
陸地導航中,方位角通常以α表示,並定義為從北基線或子午線測得的水準角。更廣義地,方位角是從任何基準面或基準方向,順時針量測的水準角。
基準面與方位角
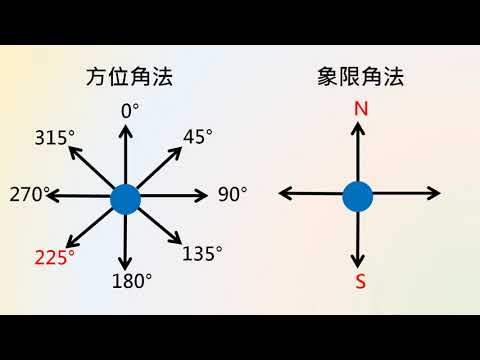
當今,方位角基準面通常以真北為0°,並順時針量測角度。然而,可使用其他角度單位,如梯度、密位。在360度圓週上,東為90°,南為180°,西為270°。部分導航系統使用南方為0°。定義清楚後,任何方向均可作為0°參考點。
方位角表達
方位角或羅盤方位通常在規定的系統中表示,其中0°可位於北或南,並順時針或逆時針量測角度。例如,方位角可表示為「南轉東30°」(縮寫為「S30°E」),即從南順時針旋轉30°,或從北逆時針旋轉150°。
計算方位角
當平面上兩點座標已知時,可計算地圖方位角:
方位角 = arctan(y / x)
其中:
- x = 目標點與觀測者在東西軸上的距離
- y = 目標點與觀測者在南北軸上的距離
注意:
- 與極座標系不同,方位角相對於北方是順時針。
- 如果方位角為負值,可連續增加360°,直至正值。
文章內容目錄
方位表示法:理解空間關係的關鍵
方位表示法是一種用於指示空間關係的系統,它可以確定一個物體相對於另一個物體的位置。方位表示法在日常生活中至關重要,因為它使我們能夠準確地描述和理解我們周圍的世界。
方位表示法類型
有許多不同的方位表示法類型,每種類型都使用不同的方式來指定空間關係。最常見的類型包括:
| 類型 | 描述 |
|---|---|
| 絕對方位 | 使用固定的參考點(如南北極點)來確定物體的位置。 |
| 相對方位 | 使用另一個物體作為參考點來確定物體的位置。 |
| 測量方位 | 使用角度或距離度量來確定物體的位置。 |
方位表示法應用
方位表示法在各種領域都有廣泛的應用,包括:
- 導航: 方位表示法對於導航至關重要,因為它使我們能夠確定我們的位置並確定我們必須前往的方向。
- 建築: 建築師使用方位表示法來規劃建築物的位置和設計。
- 測量: 測量員使用方位表示法來測量土地和建築物。
- 地理: 地理學家使用方位表示法來描述地球表面上的特徵和現象。
- 日常生活: 我們在日常生活中不斷使用方位表示法,例如指示方向或尋找物品。
絕對方位系統
絕對方位系統使用固定的參考點,例如南北極點,來確定物體的位置。最常見的絕對方位系統是:
- 經緯度: 經緯度系統使用水平(緯度)和垂直(經度)線來確定地球表面上的位置。
- 磁方位: 磁方位系統使用指南針來確定物體相對於地理北極的位置。
相對方位系統
相對方位系統使用另一個物體作為參考點來確定物體的位置。一些常見的相對方位系統包括:
- 角度方位: 角度方位系統使用角度來確定物體相對於參考方向的位置。
- 距離方位: 距離方位系統使用距離來確定物體相對於參考點的位置。
方位表示法的重要性
方位表示法對於理解空間關係至關重要。它使我們能夠準確地描述和理解我們周圍的世界,並有效地與他人溝通。方位表示法在許多領域都有廣泛的應用,包括導航、建築、測量、地理和日常生活。

